生成模型之Flow-based-Model(2)

生成模型Flow-Based Model（2）流模型

推导

根据生成器相关知识可知：一个最佳的生成器\(G^{*}= argmax_{G} \sum\limits_{i=1}^{m}logP_{G}(x^{i})\)

根据可变理论有：\(P_G(x^i)=\pi(z^i)|\det(J_{G^{-1}})|\), 其中\(z^i=G^{-1}(x^i)\)

等号两侧取对数有: \(logP_G(x^i)=log\pi(G^{-1}(x^i))+log|\det(J_{G^{-1}}|\)

由此得到最佳生成器\(G^*\)的右式, 即让\(logP_G(x^i)\)最大, 便得到最佳\(G^*\)

然而\(z^i=G^{-1}(x^i)\)对\(G\)提出了限制:

1. \(\det(J_G)\)需要可计算
2. \(G^{-1}\)要求生成器\(G\)本身可逆, 输入输出的形状一样

解决方法: 使用多个生成器\(G\)连续生成, 以达到拟合\(P_{data}\)的目的

多个生成器的情况

对于多个\(G\)的生成结果有: \(\log(P_K(x^i))=log\pi(z^i)+\sum\limits_{i=1}^Klog|\det(J_{G_{K^{-1}}})|\), 其中\(z^i=G_1^{-1}G_2^{-1}...G_K^{-1}(x^i)\)

依旧是取左式最大

流模型实质

以一个生成器为例:

graph LR
z --> G --> x

\[ logP_G(x^i)=log\pi(G^{-1}(x^i))+log|\det(J_{G^{-1}})| \]

发现为得到左式中的\(G\), 右式只是用到了\(G^{-1}\), 因此我们直接训练出\(G^{-1}\)

graph RL
x --> G-1 --> z

其中, \(x^i\)是从\(P_{data}(x)\)中采样的, \(z^i=G^{-1}(x^i)\)

欲使左式最大, 右侧两项应尽可能大

• 右侧第一项是对数函数, 而正态分布\(\pi(z^i)\)在\(z^i\)等于0向量时最大, 因此可能导致训练出的\(G^{-1}\)使所有生成的\(z^i\)都为零向量, 进而导致\(J_{G^{-1}}\)变成全零矩阵, 行列式\(\det(J_{G^{-1}})\)也为0, 最终右侧第二项变为\(-\inf\)

所以流模型实际上在做的事情就是: 在第一项趋零的情况下, 使用第二项约束结果防止全零, 最终得到最佳生成器

应用-Coupling Layer

coupling-layer

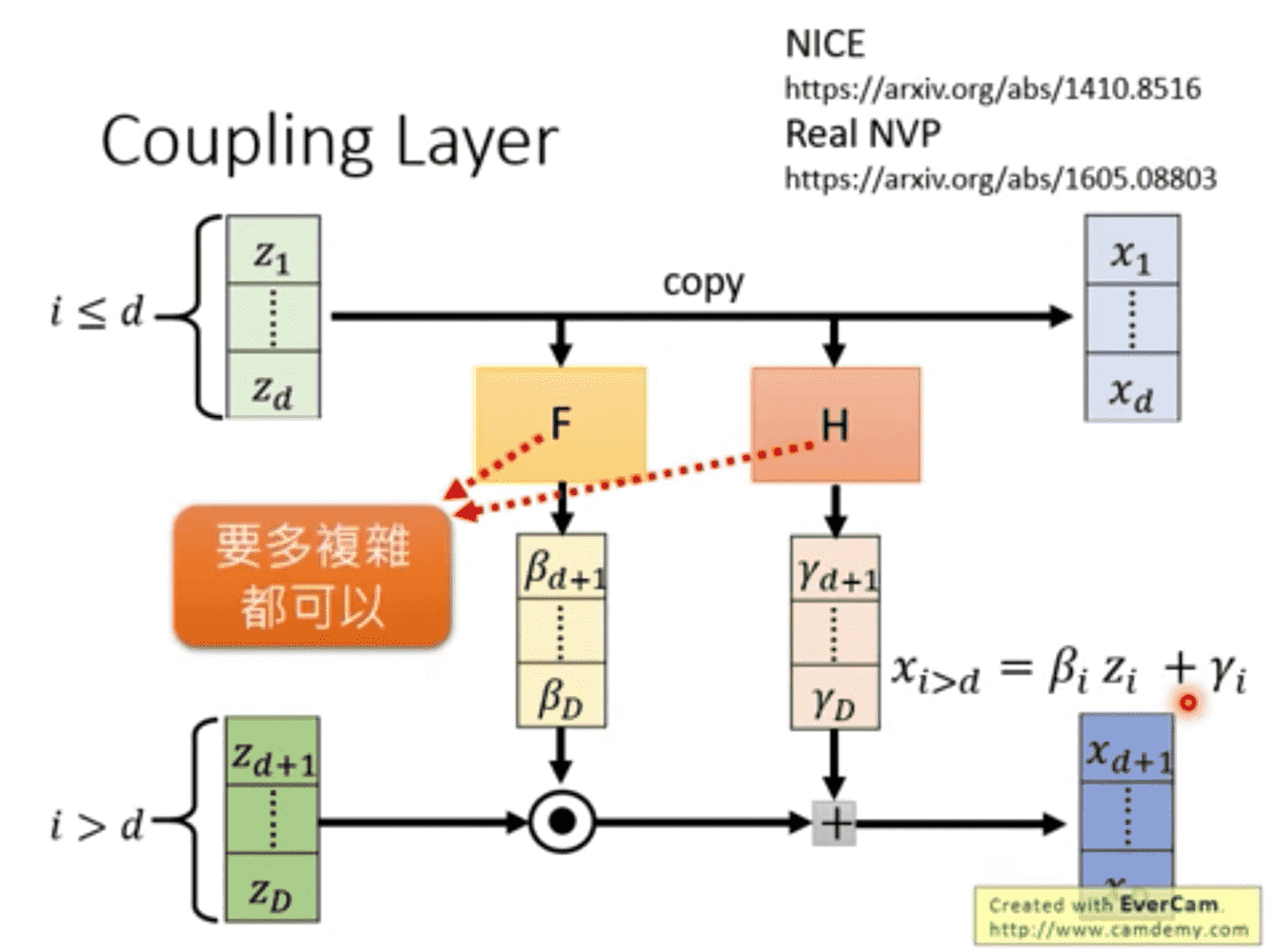
左侧为\(z^i\), 右侧为\(x^i\) \[ \begin{equation} \left\{ \begin{aligned} z_{i\leq d}&=x^i\\ z_{i > d}&=\frac {x^i-\gamma^i}{\beta^i} \end{aligned} \right. \end{equation} \]