机器学习数学基础②概率论和信息论
本文最后更新于:2022年7月31日 早上
机器学习数学基础②概率论与信息论
基础概念
随机变量:可以是连续的也可以是离散的
概率分布:符合随机变量取值范围的某个对象属于某个类别或服从某种趋势的可能性
联合概率分布:\(P(\mathrm x =x,\mathrm y=y)\)表示x=\(x\)和y=\(y\)同时发生的概率,简写为\(P(x,y)\)
概率函数和似然函数
Note:区别
对于一个函数\(P(x|\theta)\),其中x表示一个具体的数据,\(\theta\)表示模型的参数.
如果\(\theta\)已知,x为变量,这个函数就是概率函数.表示对于不同的样本点x,其出现的概率是多少.
如果x已知,\(\theta\)为变量,这个函数就是似然函数.表示对于不同的参数,出现x样本点的概率是多少.
期望:\(E(X)=\sum \limits _{k=1}^{n}x_kP(x_k), E(x)=\int xf(x)dx\)
方差:各个样本数据分别与平均数之差的平方和的平均数\(Var(x)\)
协方差:衡量随机变量X和Y之间的总体误差\(Cov(X,Y)\)
重要概念
- 条件概率:对于给定\(X=x\)时发生\(Y=y\)的概率记为\(P(Y=y|X=x)\),计算公式为\(P(Y=y|X=x)=\frac {P(x,y)}{P(X=x)}\)
- 先验概率和后验概率
- 贝叶斯公式:利用先验概率计算后验概率
Note:贝叶斯公式推导
\[ P(B|A)=\frac {P(AB)}{P(A)}, P(A|B)=\frac {P(AB)}{P(B)} \]
\[ P(AB)=P(B|A)P(A)=P(A|B)P(B) \]
\[ P(B|A)=\frac {P(B|A)P(B)}{P(A)} \]
全概率公式求\(P(A)\)
\[ P(A)=\sum \limits _{i=1}^{N}P(A|B_i)P(B_i) \]
代入得到贝叶斯公式:
\[ P(B_i|A)=\frac {P(A|B_i)P(B_i)}{\sum \limits _{i=1}^{N}P(A|B_i)P(B_i)} \]
- 最大似然估计(MLE):在”模型已定,参数\(\theta\)未知”的情况下,通过观测数据来估计未知参数\(\theta\)的一种方法,要求所有采样都是独立同分布.
- Note:最大似然估计的使用
- 写出似然函数
- 对似然函数取对数
- 两边同时求导(多个变量就求偏导)
- 令导数为0,解出似然方程
例子

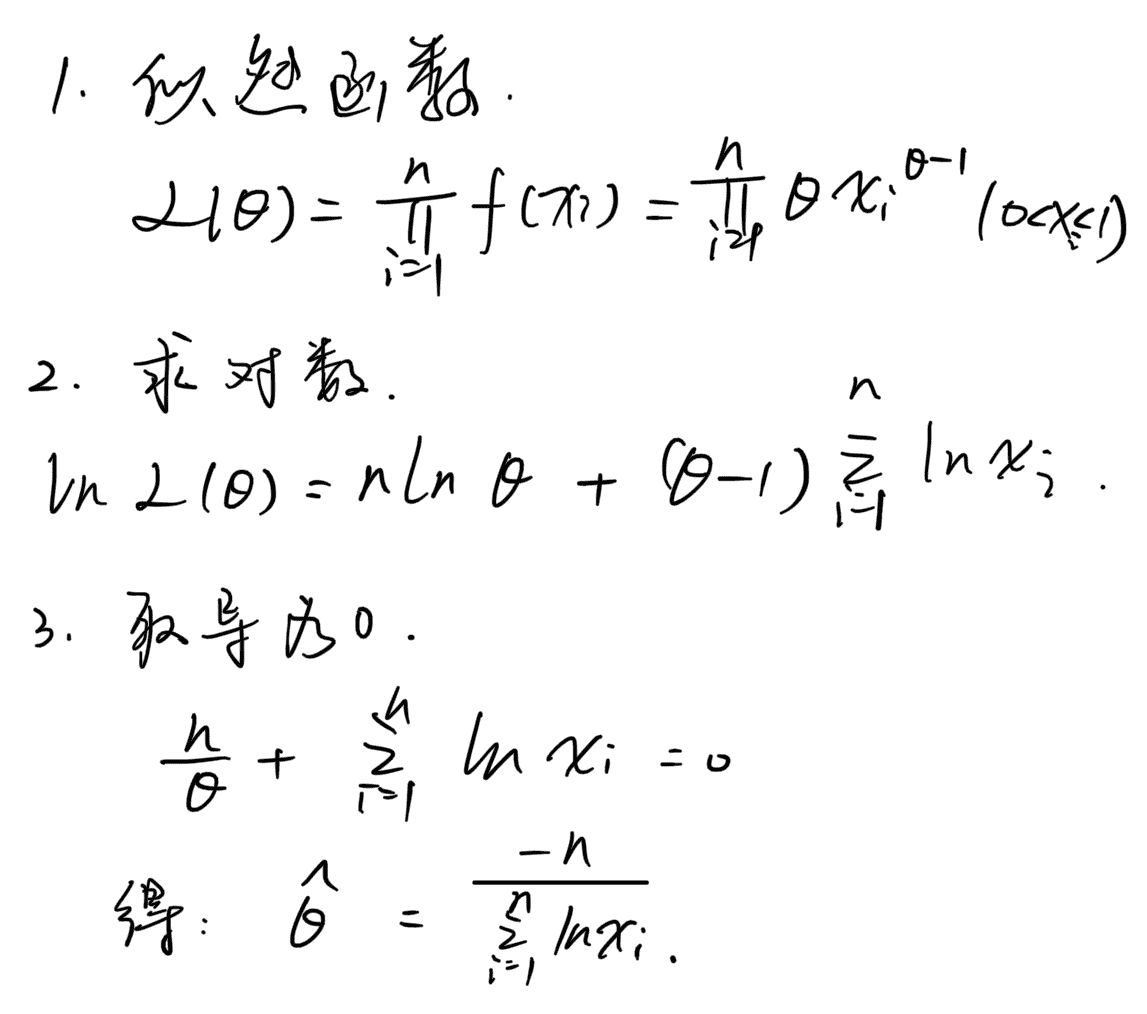
- Note:最大似然估计的使用
常见分布函数
0-1分布
\[ P(X=1)=p \\ P(X=0)=1-p \]
几何分布
离散型概率分布.在n次伯努利试验中,前k-1次失败,第k次成功的概率,其概率分布函数为:\(P(X=k)=(1-p)^{k-1}p\)
\[ E(X)=\frac {1}{p} \\ Var(X)=\frac {1-p}{p^2} \]
二项分布
n次伯努利试验中,每次试验只有两种可能结果,并且两种结果相互独立.在n次重复独立试验中事件发生k次的概率为:\(P(X=k)=C_n^kp^k(1-p)^{n-k}\) \[ E(X)=np \\ Var(X)=np(1-p) \]
高斯分布/正态分布
ML中最常用的概率分布.其中 \(\mu\)决定分布中心的位置,\(\sigma\) 标准差决定正态分布的幅度.
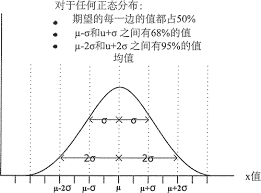
\[ X \sim N(\mu,\sigma^2) \]
指数分布
指数分布是一种连续概率分布,可以用来表示独立随机事件发生的时间间隔.其中\(\lambda >0\)表示每单位时间内发生事件的次数.
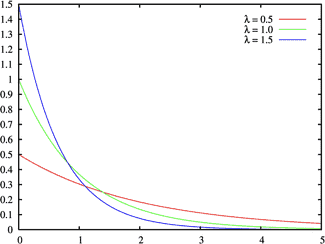
\[ X\sim Exp(\lambda) \]
概率密度函数为:
\[ f(x;\lambda)= \left\{ \begin{aligned} &\lambda e^{-\lambda x} &x\geq0 \\ &0&x<0 \end{aligned} \right. \]
特点为无记忆性,在任意时间段内某个事件发生的概率相同,结合期望理解.期望为:\(E(x)=\frac {1}{\lambda}\).
泊松分布
泊松分布是一种常见的离散概率分布.适合描述单位时间内随机事件发生的次数的概率分布.参数\(\lambda\)是随机事件发生次数的数学期望.
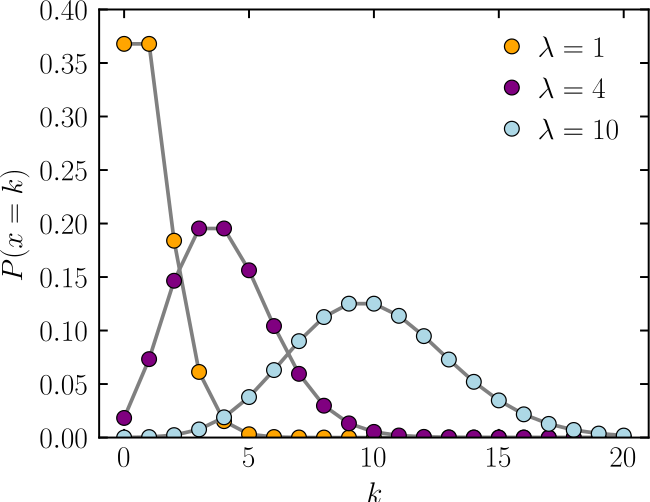
概率密度函数为:
\[ P(X=k)=\frac {e^{-\lambda}\lambda^k}{k!} \]
泊松分布表示为:
\[ X \sim Pois(\lambda) \]
性质有
期望与方差相等,都等于参数\(\lambda\)
两个独立且服从泊松分布的随机变量,其和仍然服从泊松分布
\[ X \sim Poisson(\lambda_1),Y \sim Possion(\lambda_2)\\ X+Y \sim Poisson(\lambda_1+\lambda_2) \]
信息论
自信息:
一个事件x=\(x\)的自信息为\(I(x)=-\log P(x)\)
香农熵:
一个分布P(x)的事件产生的信息总量的期望
\[ H(x)=\mathbb{E}_{X\sim P}[I(x)]=-\mathbb{E}_{X\sim P}[\log P(x)] \]
KL散度(KL divergence):
衡量两个单独的概率分布P(x)和Q(x)的差异.KL散度非负,为0时表示分布相同.
\[ D_{KL}(P||Q)=\mathbb{E}_{X\sim P}\left[ \log \frac {P(x)}{Q(x)} \right]=\mathbb{E}_{X\sim P}[\log P(x)- \log Q(x)] \]
交叉熵(cross-entropy):
\[ H(P,Q)=H(P)+D_{KL}(P||Q)=-\mathbb{E}_{X\sim P}\log Q(x) \]