机器学习数学基础③数值计算和最优化理论

数值计算

上溢和下溢

在数字计算机中我们需要通过有限的位数表示无限多的实数,这意味着会引入误差.

• 下溢(underflow):当接近零的数被四舍五入为零时发生下溢。许多函数会在其参数为零而不是一个很小的正数时才会表现出质的不同。例如，我们通常要避免被零除。
• 上溢(overflow):当大量级的数被近似为\(\infin\)或\(-\infin\)时发生上溢。进一步的运算通常将这些无限值变为非数字。

避免数值上溢或者下溢的方法常用softmax函数.

softmax函数

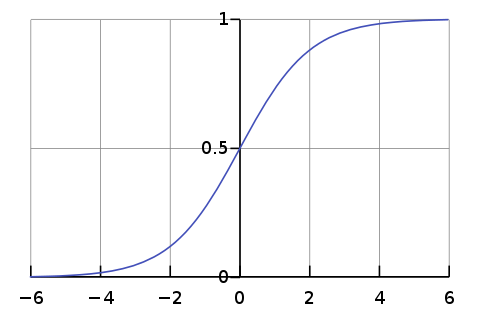
softmax函数能够将上下接近溢出的数据压缩至0-1的范围内.

最优化

最优化理论

经验风险最小化

用最小的代价取得最大的收益.也就是我们今天常说的算法.

凸集与凸集分离定理

1.凸集

在实数域的向量空间中.如果一个集合中任意两点的连线上的点都在该集合中,则该集合为凸集.

凸集和非凸集

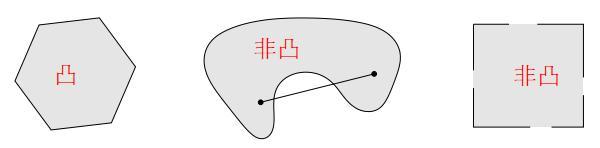
数学定义: 一个集合\(S\subset R^T\),若对于任意两点\(x,y \in S\),以及实数\(\lambda(0\leqslant \lambda \leqslant 1)\),都有\(\lambda x+(1-\lambda )y \in S\),则称集合S为凸集.

2.超平面和半空间

三维空间的超平面就是一个面(曲面),二维空间的超平面就是一条线(曲线),推广到n维空间.

超平面的某一个方向的所有样本组成半空间.

3.凸集分离定理

所谓两个凸集分离，直观地看是指两个凸集合没有交叉和重合的部分，因此可以用一张超平面将两者隔在两边，如下图所示：

凸集分离

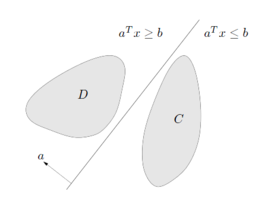
4.凸函数

凸函数是一个定义域在某个向量空间的凸子集上的实值函数.

凸函数

💡 在图中直线始终在凸函数曲线上方

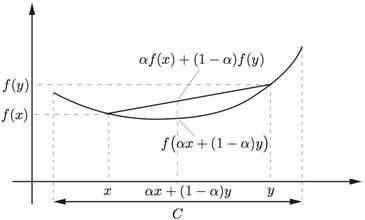
数学定义:对于函数f(x),如果其定义域C是凸集,且对于\(\forall x,y \in C, 0\leqslant \alpha \leqslant 1\),有:

\[ f(\theta x+(1-\theta )y)\leqslant \theta f(x)+(1-\theta )f(y) \]

如果一个函数是凸函数,则其局部最优点就是其全局最优点.

因为在ML中我们就是在求模型的全局最优点,所以一旦证明ML模型中的损失函数为凸函数,相当于我们只需要求它的局部最优点.

💡 求解非凸函数的全局最优点也就成了神经网络中的常见难题.