生成模型之VAE
本文最后更新于:2023年3月21日 下午
生成模型之Variational Auto-Encoder
本篇内容主要参考台大李宏毅教授的视频,作为笔记使用
【機器學習2021】自編碼器 (Auto-encoder) (上) - 基本概念
ML Lecture 18: Unsupervised Learning - Deep Generative Model (Part II)
Auto-Encoder自动编码器
压缩自动编码器
graph LR
高维图片 --> NN-Encoder --> 低维向量 --> NN-Decoder--> 生成图 --越接近越好-->高维图片
降噪自动编码器
graph LR
原图.-原图+噪声
原图+噪声 --> NN-Encoder --> 低维向量 --> NN-Decoder--> 生成图 --与原图越接近越好-->原图
解缠(Feature Disentangle)
输入信息常常由各种信息纠缠在一起,如
- 图片中存在物体、纹理
- 声音中存在文本内容、说话人信息
- 一句话包含格式、语法
- ……
这时候需要通过解缠得到不同维度包含的信息
应用:Voice Conversion语者转换
VAE变分自动编码器
AE和VAE区别
Auto-encoder
graph LR
高维图片 --> NN-Encoder --> 低维向量 --> NN-Decoder--> 生成图
VAE
是在自动编码器的基础上做变分处理,使编码器的输出为目标分布的均值方差。
graph LR
input --> NN-Encoder --> mu
NN-Encoder --> sigma
sigma --exp--> times((相乘))
e --> times
mu --> plus((相加))
times -->plus
plus --> z -->
NN-Decoder--> output
其中mu、sigma、e、z均为向量,并且e内元素服从正态分布,\(z_i=\exp(\sigma_i)\times e_i + \mu_i\)
mu是均值,e是噪声,sigma代表噪声的大小即variance方差,z就是目标概率分布。为避免variance方差被生成为0,即没有噪声,需要加上限制条件。
所以需要最小化如下函数:
\[ \min \sum \limits _{i=1} ^n (\exp(\sigma_i)-(1+\sigma_i)+\mu_i^2) \]
VAE推导
高斯混合模型(GMM)
部分内容参考
高斯混合模型是单一高斯概率密度函数的延伸,由于GMM能够平滑的近似任意形状的密度分布,因此常用在语音领域。
GMM的工作就是将复杂的P(x)分布变为多个高斯分布的混合,当拆分的越多时,越接近原始P(x)分布。
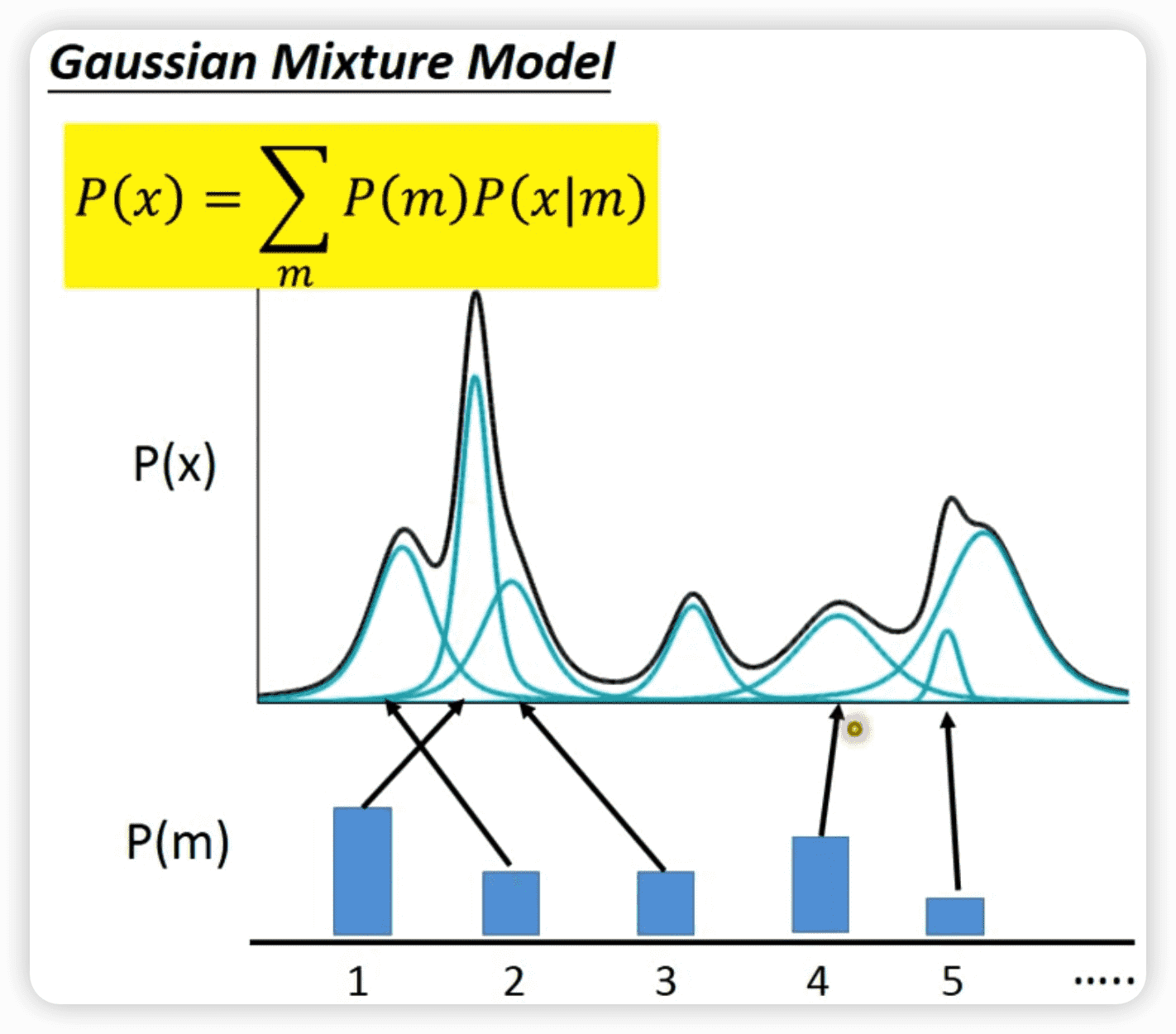
如果用每一组高斯分布的取值作为一个维度,就可以用m表示第几个维度,如果有512维,m的取值就是1,2,3……512
从多项式分布P(m)中采样一个整数m,表示一个高斯分布\(N(\mu^m,\sigma^m)\),P(x)可表示为所有这些高斯分布的和:
\[ P(x)=\sum \limits _mP(m)P(x|m) \]
其中,\(m\sim P(m)\),\(x|m \sim N(\mu^m,\sigma^m)\)
不过这种混合方式是离散的,还存在失真的地方,于是我们将其转化为连续的。
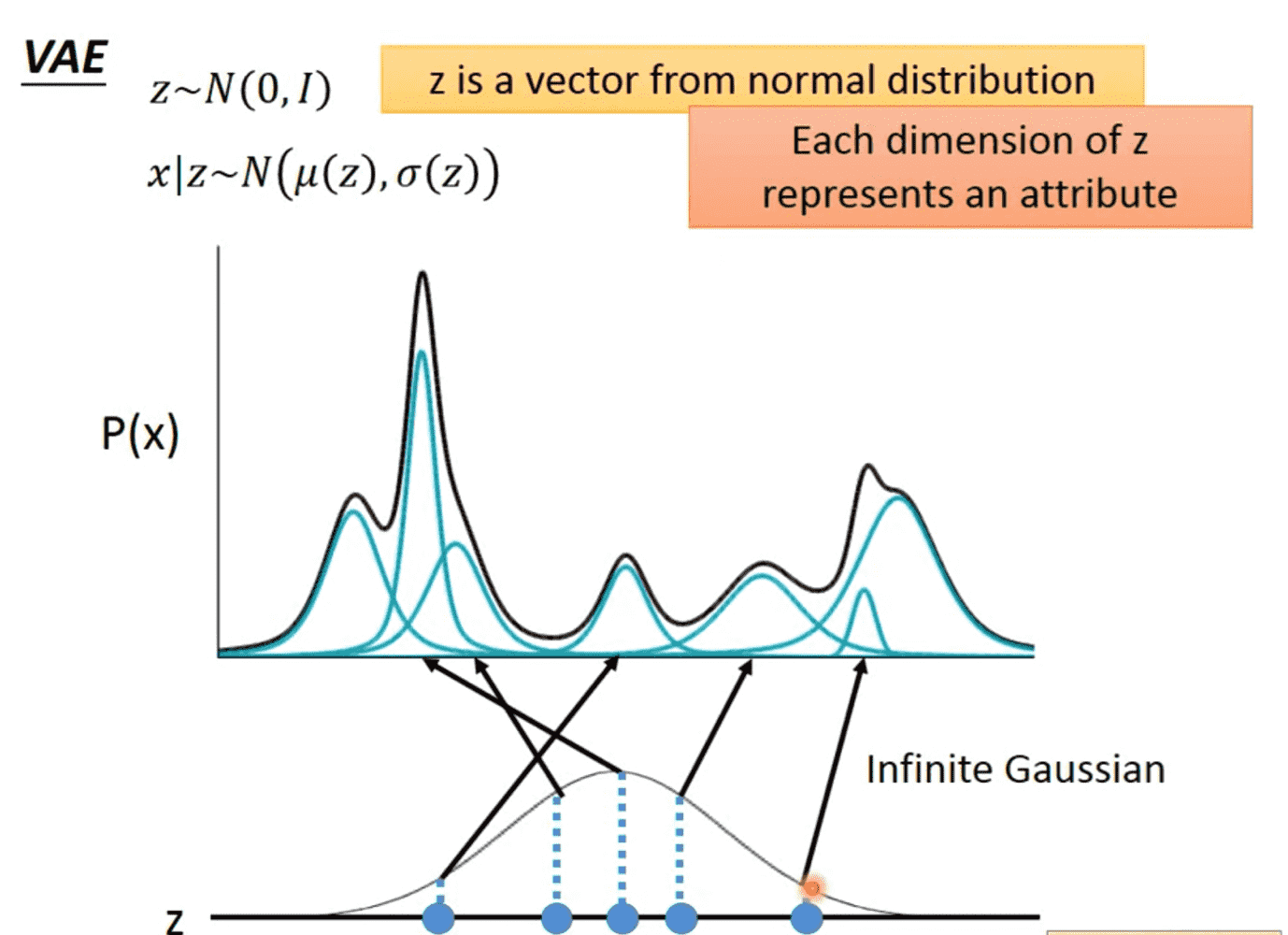
现在将离散变量m改为连续变量z,依旧是z的某一个取值对应一个高斯分布。
\(z\sim N(0,I)\),\(x|z\sim N(\mu(z),\sigma(z))\),其中\(\mu\)是得到z均值的函数,\(\sigma\)是得到z方差的函数。
于是P(x)的分布就可以表示为:
\[ P(x)=\int\limits _zP(z)P(x|z)dz \]
所以我们的目标就变成求解上面这个公式。
求解目标公式
\[ P(x)=\int\limits _zP(z)P(x|z)dz \]
其中\(P(z)\)已知,\(P(x|z)\)未知,\(P(x|z)\)中\(x|z\sim N(\mu(z),\sigma(z))\),所以求解\(P(x|z)\)转换为求解\(\mu,\sigma\)两个函数的表达式。
如何求解\(\mu,\sigma\)函数?使用神经网络!
graph LR
z --> NN-Decoder --> mu
NN-Decoder --> sigma
同时我们再加上一个新的函数\(q(z|x)\)用来表示任意高斯分布,其中\(z|x \sim N(\mu'(x),\sigma'(x))\),表示对于一个输入的x,能够得到一对均值和方差,用于生成z的概率分布。
graph LR
x --> NN-Encoder --> mu'
NN-Encoder --> sigma'
因为实际上我们有数据x,现在是在求解参数,所以需要求\(P(x)\)的最大似然函数\(L=\sum \limits _x \log P(x)\)
- 最大似然估计(MLE):在”模型已定,参数\(\theta\)未知”的情况下,通过观测数据来估计未知参数\(\theta\)的一种方法,要求所有采样都是独立同分布.
- Note:最大似然估计的使用
- 写出似然函数
- 对似然函数取对数
- 两边同时求导(多个变量就求偏导)
- 令导数为0,解出似然方程
例子

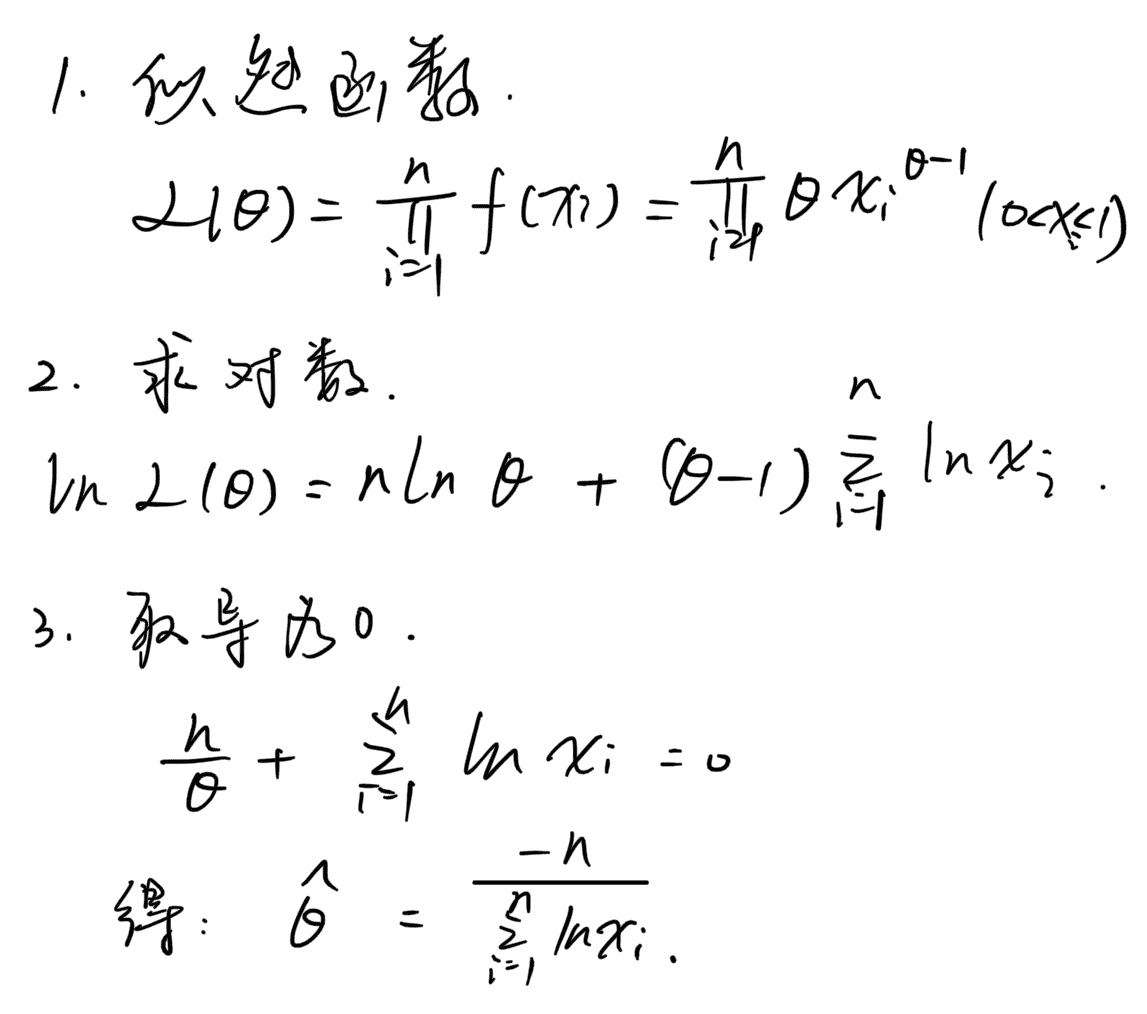
- Note:最大似然估计的使用
由于\(q(z|x)\)是一个任意的高斯分布,于是有\(\int \limits _z q(z|x)dz=1\),表示整个高斯分布的面积为1。
\[ \begin{aligned} \log P(x) &=\int \limits _zq(z|x)\log P(x)dz \\ &=\int \limits _zq(z|x)\log \big(\frac{P(x|z)P(z)}{P(z|x)}\big)dz \\ &=\int \limits _zq(z|x)\log (\frac{P(x|z)P(z)}{q(z|x)}\cdot\frac{q(z|x)}{p(z|x)})dz \\ &= \int \limits _zq(z|x)\log(\frac{P(x|z)P(z)}{q(z|x)})dz + \int \limits _zq(z|x)\log(\frac{q(z|x)}{P(z|x)})dz \\ &= \int \limits _zq(z|x)\log(\frac{P(x|z)P(z)}{q(z|x)})dz +KL(q(z|x)||P(z|x)) \end{aligned} \]
最后得到两项,第二项KL散度非负,所以第一项就是结果的下界\(L_b\)
\[ \log P(x) \geqslant \int \limits _z q(z|x)\log(\frac{P(x|z)P(z)}{q(z|x)})dz \]
\[ \log P(x) = L_b+KL(q(z|x)||P(z|x)) \]
这里将原本的问题:求\(P(x|z)\)使得\(\log P(x)\)最大化
转换为了新的问题:求P(x|z)和q(z|x)使得\(\log P(x)\)最大化
看起来像是多了一个\(q(z|x)\),其实不然,我们开始观察\(\log P(x)\)跟这两项的关系:
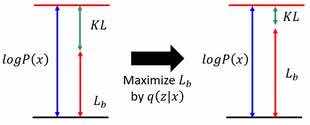
根据\(P(x)=\int\limits _zP(z)P(x|z)dz\):
当我们保持\(P(x|z)\)不变时,\(P(z)\)不会变,\(P(x)\)也不会变,\(\log P(x)\)也不会变
再根据\(\log P(x) = L_b+KL(q(z|x)||P(z|x))\):
整个\(\log P(x)\)的大小不变,\(L_b\)越大,KL散度越小,当KL散度减小到零时,\(\log P(x)=L_b\),而\(L_b\)此时只和\(q(z|x)\)有关。
此时我们发现:
求\(\max \log P(x)\)等价于求\(\max L_b\)
VAE算法:Decoder每改进一次,Encoder就调节成与其一致,利用约束条件逼迫Decoder前进
开始求解\(\max L_b\)
\[ \begin{aligned} L_b &= \int \limits _zq(z|x)\log (\frac {P(x|z)P(z)}{q(z|x)})dz \\ &= \int \limits _zq(z|x)\log (\frac {P(z)}{q(z|x)})dz + \int \limits _zq(z|x)\log P(x|z)dz \\ &=-KL(q(z|x)||P(z))+\int \limits _zq(z|x)\log P(x|z)dz \end{aligned} \]
记第一项为A,第二项为B,现在求解\(L_b\)的最大值,需要求A的最大值(KL散度的最小值),B的最大值
展开A后可以得到约束项:\(\min \sum \limits _{i=1} ^n (\exp(\sigma_i)-(1+\sigma_i)+\mu_i^2)\),证明方法来自VAE原论文《Auto-Encoding Variational Bayes》
求B的最大值:
\[ \max B = \max E_{q(z|x)}[\log P(x|z)] \]
可理解为提供一个x的值,在\(q(z|x)\)这个分布下,让\(\log P(x|z)\)值越大越好,这件事情就是NN-Encoder在做的。
graph LR
x --> NN-Encoder --> mu'
NN-Encoder --> sigma'
mu'-->z
sigma'-->z
z-->NN-Decoder-->mu
NN-Decoder-->sigma
mu .-越接近越好.-> x
VAE的损失函数的两部分,一是重建损失,二是约束项。